درباره من
نظرسنجی
نظر شما در مورد وبلاگ چیست ؟
نظرسنجی
چرا ریاضی برای شما سخت است ؟
روزانهها
همه- بازیهای زیاضی جالبه !
- مترجم از انگلیسی به فارسی و فارسی به انگلیسی
- انجمن معلمان ریاضی استان قزوین
- وبلاگ تخصصی مهندسی مکانیک
- نرخ پول کشورمان در برابر کشورهای دیگر !
- دانستنیهای علوم تجربی
- صدای ریاضی
- انجمن نجوم هوا وفضای آسمانز
- آخرین جرعه جام آهنگهای از استاد شجریان و ...
- یک سایت افغانی جالب
- قران و شعر کهن بصورت آنلاین
- آهنگهای از استاد شجریان
- اطلاعات دقیق از اخبار ورزشی ایران و جهان
- سرزمین آرزوها
- فوتبال ایران
- مسایل المپیادهای ریاضی جهانی
- خط نستعلیق را تمرین کنید
- یک وب سایت جستجو در زمینه قران ، شاهنمامه ، دیوان حافظ ، دیوان سعدی و ... می توانید در این سایت سرچ کنید .
- مجموعه ای مناسب از سایتهای ایرانی
- وضعیت آب و هوای شهرهای ایران
- سایتی مخصوص کودکان در این سایت مطالب متنوع از قبیل بازیهای فکری ؛سرگرمی ، شعر و داستان و ... برای کودکان وجود دارد ؛فقط کودکان!!.
- ستاد ویژه فن آوری نانو در این سایت جدیدترین پیشرفتهای نانو تکنولوژی را مشاهده کنید.
- فکر می کنید چقدر عمر می کنید ؟ نترسید کلیک کنید این سایت انگلیسی است و از شما اطلاعاتی را گرفته و عمر شما را پیش بینی می کند ، بااینکه این سایت علمی است ولی الله و اعلم .
- محاسبات هندسی بصورت آنلاین در این سایت می توانید محاسبات هندسی مانند مساحت و محیط و ... را آنلاین انجام دهید.
- محاسبه میانگین ؛میانه ؛ مد و دامنه تغییرات بصورت آنلاین
- موسسه سروش رسانه در این سایت می توانید برنامه تلویزیون شبکه های سراسری را بصورت زنده و یا در آرشیو مشاهده کنید .
- دانشکده ریاضی دانشگاه شریف
- راهنمای شماره تلفن افراد در تمام ایران
- ضریب هوشی خود را مشخص کنید .
- حل انتگرال بصورت آنلاین در این قسمت می توانیدجواب انتگرال نامعین را بصورت آنلاین مشاهده کنید .
پیوندها
- ::..مـــثـلـث..::
- ::..امید ریاضی..::
- ::..آبگینه ساری..::
- ::..آموزش ریاضی..::
- ::..استاد شجریان..::
- ::..هندسه فضایی..::
- ::..واژه های زندگی..::
- ::..آموزش ریاضی ۲..::
- ::..روانشناسی کودک..::
- ::..کار ایران - امیر حسین..::
- ::..همجوشی هسته ای..::
- ::..روانشناسی و مشاوره..::
- ::..ریاضی سلطان علوم است..::
- ::..ایرانـیـان مقیـم خارج از کشــور..::
- :..مدرسه جمهوری اسلامی در توکیو..:
- :.گروه علوم اجتماعی راهنمایی البرز.:
- :.ریاضی و حل مسایل موسیقی فــکر.:
- کمیته برنامه ی درسی ملی استان قزوین
- :.مدرسه جمهوری اسلامی در استکهلم.:
- :.گروه ریاضی متوسطه هشترود.:
- ریاضی اگر و تنها اگر زیبایی
- :.بانک مرجع و سرگرمی.:
- **شیرینی زندگی**
- :..شخصی..:
- آموزش رجیستری
- انجمن معلمان ریاضی استان قزوین
دستهها
برگهها
جدیدترین یادداشتها
همه- اثبات :
- بزرگترین عدد اول :
- ده مطلب زیر را هیچگاه فراموش نکنید .
- بدون متن :
- [ بدون عنوان ]
- نمونه سوال جبر احتمال:
- حل معمای مکعب روبیک در حداکثر 20 حرکت امکان پذیر است :
- قضیه فشردگی :
- طنز ریاضی :
- ابداع مدلی برای پیش بینی طول عمر:
- سخنی با مسئولین :
- دنیای ریاضی در فضای نانو:
- عید نوروز مبارک :
- خورشید گرفتگی و ۱۰ پدیده جالب :
- برترین ها در ریاضیات :
- به یاد سالار شهیدان :
- ساده کردن بعضی از دانشجویان !!!!
- عید غدیر خم بر مسلمین جهان مبارک :
- نگاهی به زندگی ارشمیدس :
- هندسه ترسیمی و رقومی :
- به دانش آموزان و دانشجویان چه مطالبی بیاموزیم :
- ۵۰ سوال در حساب و دیفرانسیل :
- لیستی از چند سایت جالب :
- تبریک:
- کتاب ریاضی ۲ جدید التالیف :
- زندگینامه دانشمندان ریاضی (قسمت اول ):
- مورچه ها هم ریاضی می دانند
- هشتاد توصیه بسیار مهم به معلمین عزیز :
- نقد و بررسی انواع الگوهای تدریس ریاضیات :
- جایزه ویژه انجمن ریاضی آمریکا به استادیار ایرانی اعطا شد :
- روش حل مساله :
- [ بدون عنوان ]
- نمونه سوالات دروس پیش دانشگاهی
- حل آنلاین مسایل ریاضی:
- معلمان گرانقدر بخونند:
- [ بدون عنوان ]
- نمونه سوالات درس حسابان رشته ریاضی سال سوم :
- نمونه سوالات درس جبر احتمال همراه پاسخنامه تشریحی :
- نموانه سوالات درس جبر احتمال با پاسخنامه :
- نمونه سوالات درس حسابان با پاسخنامه :
- بزرگترین عدد اول دیگر :
- پرفسور لطفی زاده کیست ؟
- رسم نمودار تابع :
- واژه ریاضیات :
- ماه رمضان :
- تغییرات در کتابهای درسی :
- از حافظ دلسوخته :
- حدس بزنید :
- دو آهنگ زیبا از استاد شجریان :
- برگی از یک نوشته :
نویسندگان
- جوادی 109
بایگانی
- اسفند 1393 1
- آذر 1393 2
- فروردین 1391 1
- اسفند 1390 1
- بهمن 1390 1
- دی 1389 1
- شهریور 1389 2
- تیر 1389 1
- خرداد 1389 1
- اردیبهشت 1389 1
- اسفند 1388 1
- بهمن 1388 2
- آذر 1388 6
- آبان 1388 2
- مرداد 1388 4
- خرداد 1388 2
- اردیبهشت 1388 1
- اسفند 1387 2
- دی 1387 1
- آذر 1387 4
- آبان 1387 3
- مهر 1387 1
- شهریور 1387 4
- مرداد 1387 3
- تیر 1387 4
- اردیبهشت 1387 3
- فروردین 1387 6
- اسفند 1386 4
- بهمن 1386 1
- دی 1386 4
- آذر 1386 10
- آبان 1386 8
- مهر 1386 10
- شهریور 1386 3
- مرداد 1386 6
- تیر 1386 2
آمار : 356529 بازدید
Powered by Blogsky
اثبات :
ثابت کنید 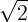 گنگ است.
گنگ است.
اثباتی که اکثر دوستان علی الخصوص دانش آموزان دبیرستانی دیده اند اثباتی نظریه ی اعدادی بوده است در این پست اثباتی متفاوت را برای شما عزیزان ارائه خواهم داد امّا قبل از هر چیز لازم می دانم اصل خوشترتیبی را یادآوری نمایم.
اصل خوشترتیبی(اعداد طبیعی):هر زیر مجموعه ی غیر تهی از اعداد طبیعی عضو ابتدا(کوچکترین عضو) دارد.
اثبات: فرض کنیم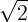 گنگ نباشد(فرض خلف) پس
گنگ نباشد(فرض خلف) پس 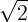 گویا است .اکنون مجموعه ی
گویا است .اکنون مجموعه ی  را به صورت زیر تعریف می کنیم:
را به صورت زیر تعریف می کنیم:
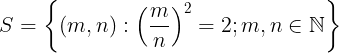
اثباتی که اکثر دوستان علی الخصوص دانش آموزان دبیرستانی دیده اند اثباتی نظریه ی اعدادی بوده است در این پست اثباتی متفاوت را برای شما عزیزان ارائه خواهم داد امّا قبل از هر چیز لازم می دانم اصل خوشترتیبی را یادآوری نمایم.
اصل خوشترتیبی(اعداد طبیعی):هر زیر مجموعه ی غیر تهی از اعداد طبیعی عضو ابتدا(کوچکترین عضو) دارد.
اثبات: فرض کنیم
طبق اصل خوشترتیبی 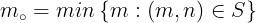 کوچکترین عضو مجموعه ی صورت ها می
کوچکترین عضو مجموعه ی صورت ها می
باشد. فرض کنیم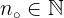 ی موجود باشد بطوریکه
ی موجود باشد بطوریکه 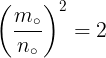 در اینصورت داریم:
در اینصورت داریم:
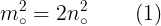
باشد. فرض کنیم
اکنون با کم کردن عبارت 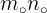 از طرفین رابطه ی
از طرفین رابطه ی 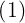 نتیجه می شود:
نتیجه می شود:
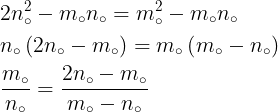
چون 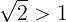 پس
پس 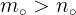 و از اینجا نتیجه می شود
و از اینجا نتیجه می شود 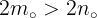 و یا
و یا 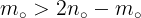 .یعنی
.یعنی 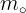 کوچکترین عضو مجموعه ی صورت ها نیست و این یک تناقض است . چون
کوچکترین عضو مجموعه ی صورت ها نیست و این یک تناقض است . چون 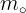 و
و 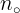 ی یافت نمی شوند که در شرایط مجموعه
ی یافت نمی شوند که در شرایط مجموعه 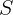 صدق کنند بنابراین
صدق کنند بنابراین 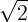 گنگ است.
گنگ است.